
Recently, I had the urge to be lazy and have the computer do my work for me. I was designing some 8×8 graphics characters for the Commodore VIC-20 and wanted one for each offset position in a 2-character block (see image to the right).
Using modern tools like the Windows-based CBM prg Studio I could have easily edited each one by hand to get the desired result (which is what I did to create that image), but I thought it might be more fun to just design one character and write a program to create the other shifted frames.
I have bit shifted in C programming many times (because it has a bit shift operator) but I don’t recall ever knowingly doing it in BASIC.
Bit shifting basics
Bit shifting is where you take all the bits in a byte (or word, or long, whatever) and move them left or right. Here is an example of shifting the byte value 00111100 to the right:
Before: [ 0 0 1 1 1 1 0 0 ] After : [ 0 0 0 1 1 1 1 0 ]
If you just want to shift and don’t care about the bit that “falls off the edge,” it is as simple as multiplying or dividing the value by 2.
To demonstrate this, we first need a program that will display a byte as bits.
0 REM bitsslow.bas
10 Z=&H00:GOSUB 500
20 Z=&HF0:GOSUB 500
30 Z=&H0F:GOSUB 500
40 Z=&HFF:GOSUB 500
50 END
500 REM PRINT BITS
510 FOR ZB=7 TO 0 STEP -1
520 IF Z AND 2^ZB THEN PRINT"1"; ELSE PRINT "0";
530 NEXT
540 PRINT:RETURN
The routine at line 500 will print the value in variable Z as bits. It is hard coded to only work with a byte (0-255). When I run that, this is what it displays:
00000000 11110000 00001111 11111111
Those lines correspond to &H00, &HF0, &H0F and &FF. I show them in hex so the bit pattern is easier to see (0=0000, F=1111).
A bit faster…
My bit printing routine is so slow that you can see it print the digits one at a time. This is due to the math that goes on in line 520 for each bit check. To speed things up, we could pre-calculate an array of those powers of two (1, 2, 4, 8, 16, 32, 64, 128) and use that instead:
0 REM bitsfast.bas
5 GOSUB 1000
10 Z=&H00:GOSUB 500
20 Z=&HF0:GOSUB 500
30 Z=&H0F:GOSUB 500
40 Z=&HFF:GOSUB 500
50 END
500 REM PRINT BITS
510 FOR ZB=7 TO 0 STEP -1
520 IF Z AND ZB(ZB) THEN PRINT"1"; ELSE PRINT "0";
530 NEXT
540 PRINT:RETURN
1000 REM INIT BIT ARRAY
1010 FOR ZB=0 TO 7
1020 ZB(ZB)=2^ZB
1030 NEXT
1040 RETURN
Line 5 will GOSUB to our initialization routine which sets up the power-of-two array ZB(). After that, the routine at 500 can be called as it previously was, except now it will print so fast you can’t really see it printing.
Now let’s use this routine to demonstrate bit shifting by multiplying or dividing by 2.
Bit shifting left
0 REM bitshftl.bas
5 GOSUB 1000
10 Z=1 '00000001
20 FOR A=1 TO 8
30 GOSUB 500
35 REM *2 TO SHIFT LEFT
40 Z=Z*2:NEXT
50 END
500 REM PRINT BITS
510 FOR ZB=7 TO 0 STEP -1
520 IF Z AND ZB(ZB) THEN PRINT"1"; ELSE PRINT "0";
530 NEXT
540 PRINT:RETURN
1000 REM INIT BIT ARRAY
1010 FOR ZB=0 TO 7
1020 ZB(ZB)=2^ZB
1030 NEXT
1040 RETURNIn line 10, Z starts out with 1, which is the bit pattern of 00000001. It is then multiplied by 2 in a loop eight times, each time shifting the bit one place to the left. The output looks like this:
00000001 00000010 00000100 00001000 00010000 00100000 01000000 10000000
Bit shifting right
And if we start out with Z being 128 (bit pattern 10000000) and divide by 2, it will shift right:
0 REM bitshftr.bas
5 GOSUB 1000
10 Z=128 '10000000
20 FOR A=1 TO 8
30 GOSUB 500
35 REM /2 TO SHIFT RIGHT
40 Z=Z/2:NEXT
50 END
500 REM PRINT BITS
510 FOR ZB=7 TO 0 STEP -1
520 IF Z AND ZB(ZB) THEN PRINT"1"; ELSE PRINT "0";
530 NEXT
540 PRINT:RETURN
1000 REM INIT BIT ARRAY
1010 FOR ZB=0 TO 7
1020 ZB(ZB)=2^ZB
1030 NEXT
1040 RETURN
This will display:
10000000 01000000 00100000 00010000 00001000 00000100 00000010 00000001
Pretty simple. And if that were all I wanted to do, I’d be done.
But that was not all I wanted to do, so I am not done.
I wanted to shift bits right in one byte and have the bits that shift out end up shifting in to a second byte, like this:
1st Byte 2nd Byte 1) [00001111][00000000] 2) [00000111][10000000] 3) [00000011][11000000] 4) [00000011][11100000] 5) [00000001][11110000] 6) [00000000][11111000] ...etc...
I spent far too much time coming up with an approach that would get me which bits were going to be shifted off to the right (using AND), and then placing those in a new variable and then shifting those bits to the left to line up where they would have ended up if I had just shifted a 16-bit value…
…then I realized that was silly, because I could just use a 16-bit value in BASIC!
16-bits in BASIC
You may have seen things like this which print out memory locations BASIC is using:
PRINT PEEK(25)*256+PEEK(26)
In Color BASIC, memory locations 25 and 26 contain the 16-bit address for where BASIC memory starts. Since PEEK only works on a single byte, it takes two PEEKs to get the two bytes that make up the 16-byte address, and some math to turn the two 8-bit values into one 16-bit value.
On my virtual CoCo in the Xroar emulator, memory location 25 contains 38 (&H26) and memory location 26 contains 1 (&h01). To turn those two 8-bit values into a 16-bit address, I need to somehow shift the 38/&H28 left eight times into a new 16-bit value, and then add (or OR) in the 1/&H01 value.
In C, one of the ways we’d do this is by using the bit shift operator:
uint16_t Result;
uint8_2 Byte1;
uint8_2 Byte2;
Byte1 = Peek(25); // Made up function to get a memory value.
Byte2 = Peek(26);
Result = (Byte1 << 8) | Byte2; // Shift Byte1 left 8 bits,
// OR in Byte2.
// Or...
Result = (Byte1 << 8) + Byte2; // Since the right 8 bits are empty,
// adding would have the same result.
…but there are many other ways to do the same thing, some much faster than these two approaches.
Back to BASIC
Shifting left can be done by multiplying the value by 2. To shift once, you might have:
V = V * 2To shift twice, you could do:
V = V * 2 * 2…but that looks silly. You’d just multiply by 4. And to bit shift three places (2 * 2 * 2) you could multiply by 8. See the pattern? They are all powers of 2 (2, 4, 8, 16, 32, 64, 128, 256, etc.)
So to shift 8 places left, you multiply by 256. Thus, the C example I gave earlier is represented in BASIC by:
10 B1=PEEK(25)
20 B2=PEEK(26)
30 R=(B1*256)+B2Tada! When I first saw things like “X=PEEK(Y)*PEEK(Z)” back then, I did not understand why it worked, I just knew it did. And I was also confused at why the CoCo was like that, since on the VIC-20 it would have been “X=PEEK(Y)+256*PEEK(Z)”. See the differences? On the CoCo’s 6809 processor, a 16-bit value is YYZZ, but on the VIC-20’s 6502 processor it is stored the opposite as ZZYY. Thus, on my VIC, you would take the second location and multiply it by 256 then add the first location.
But I digress.
A bit more…
The previous example shows how you are effectively shifting a byte (B1) left 8 places so it ends up at the top 8-bits of a new 16-bit value. Something like that would work very well for shifting an 8-bit value into different positions of two characters (two bytes).
My approach would be this:
- R will be the result, a value representing 16-bits (two bytes, 0-65535 in range).
- Since I am shifting right (in this example), my first step is to get the 8-bit source value into the top 8-bits (left most bits) of the R result variable.
- Next I will shift that entire R variable to the right, and then extract the left and right 8-bits as separate variables which is my output values.
Extract? Well, that will be the reverse of what we just did. In C, you can turn a 16-bit value into two 8-bit values like this:
uint16_t Source; uint8_2 Byte1; uint8_2 Byte2; Source = 0x1234; // Some 16-bit value. Byte1 = (Source >> 8); // Shift left 8-bits to the right. Byte2 = (Source & 0x00ff); // Mask off top 8-bits.
…though there are many other (faster/better ways to do this). But, we could do this in BASIC the same way.
If shifting left is multiplying by 256, then shifting right must be dividing by 256.
10 R=&H1234
20 B1=(R/256)
30 B2=(R AND &HFF)IMPORTANT NOTE: As I got to a later point in this article, I discovered a huge problem with this approach. If you didn’t already know it (I didn’t), I’ll explain it in just a bit… When I write, I’m usually learning as I type, and I decided to keep this stream of consciousness intact.
That is the first time I’ve ever done it that way in BASIC (duplicating the way C does it). The way I’ve commonly seen it done in BASIC is this:
10 R=&H1234
20 B1=INT(R/256)
30 B2=R-(B1*256)Here is a simple test program:
0 REM split1.bas
10 S1=&H12
20 S2=&H34
30 R=S1*256+S2
40 PRINT HEX$(S1)" "HEX$(S2)" -> "HEX$(R)
50 D1=INT(R/256)
60 D2=R-(D1*256)
70 PRINT HEX$(R)" -> "HEX$(D1)" "HEX$(D2)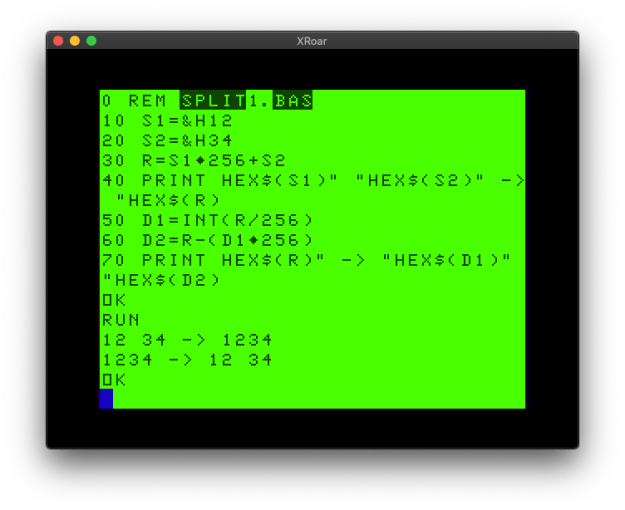
Benchmark digression
Have I been doing it wrong since the 1980s? Is the C-style way (using AND) any faster than the BASIC way (using INT)? Let’s try the C-style way using my trusty benchmark program:
0 REM split2.bas
5 DIM TE,TM,B,A,TT
6 R=&H1234
10 FORA=0TO3:TIMER=0:TM=TIMER
20 FORB=0TO1000
30 IF Z=42 THEN 100
40 B1=R/256
50 B2=R AND &HFF
70 NEXT
80 TE=TIMER-TM:PRINTA,TE
90 TT=TT+TE:NEXT:PRINTTT/A:END
This shows 1143. (Of course it could be made faster using hex and removing spaces and such, but this is just for comparison with the second version.)
And now let’s try it the traditional BASIC:
0 REM split3.bas
5 DIM TE,TM,B,A,TT
6 R=&H1234
10 FORA=0TO3:TIMER=0:TM=TIMER
20 FORB=0TO1000
30 IF Z=42 THEN 100
40 B1=INT(R/256)
50 B2=R-B1*256
70 NEXT
80 TE=TIMER-TM:PRINTA,TE
90 TT=TT+TE:NEXT:PRINTTT/A:END
This version reports 1498! Well I’ll be darned… INT and a divide and a subtract and a multiply is slow than a divide and an AND. Well, once I write it out like that, I guess it makes sense.
I suppose applying some things I learned in C to BASIC is paying off.
But I digress…
Are we there yet?
So getting back to the original task, I should be able to combine 8-bit values and split 16-bit values and shift them any way I want.
First let me modify the bit printing routine to handle 16-bit values.
IMPORTANT NOTE: Here’s the bit I was talking about earlier…
I thought I could just change the 0 to 7 into 0 to 15 to cover all 16 bits, but that resulted in an ?FC ERROR (function call). A bit of testing revealed that AND only works on values from 0 to 32767 (&H7FFF). That is the maximum value of a 16-bit SIGNED integer, which uses 15-bits for the number and 1-bit for the sign (+ or -).
Yipes! So I could only easily show 15-bits, and I really want that extra bit.
Note to Self: Look into the Color BASIC Unravelled book and see why this is.
So, it looks like I’ll just have to modify my 8-bit print routine to print each byte of a 16-bit value separately. Good thing we learned how to do that earlier in this article!
16-bit bit printing
Here is how I had to modify the routine:
0 REM bits16.bas
5 GOSUB 1000
10 Z=&H0000:GOSUB 500
20 Z=&HFF00:GOSUB 500
30 Z=&H00FF:GOSUB 500
40 Z=&HFFFF:GOSUB 500
50 END
500 REM PRINT BITS
501 ZZ=INT(Z/256):GOSUB 510
502 ZZ=Z-ZZ*256:GOSUB 510
503 PRINT:RETURN
510 FOR ZB=7 TO 0 STEP -1
520 IF ZZ AND ZB(ZB) THEN PRINT"1"; ELSE PRINT "0";
530 NEXT
540 RETURN
1000 REM INIT BIT ARRAY
1010 FOR ZB=0 TO 7
1020 ZB(ZB)=2^ZB
1030 NEXT
1040 RETURNWhew! That works, and prints the following:
0000000000000000 1111111100000000 0000000011111111 1111111111111111
Okay, so I did not discover any amazing speedup (at least if we want to use values larger than 32767), but I did get it to work.
I saved the best bit for last…
Now we can try a little test to see if we can start with an 8-bit value, shift it to the left side of a 16-bit value, the start shifting one bit at a time right, then splitting up the resulting two bytes at each step. I will use a test byte of &HFF (11111111).
0 REM shift16.bas
5 GOSUB 1000
10 Z=&HFF '11111111
15 Z=Z*256 '1111111100000000
20 FOR A=1 TO 8
25 REM SPLIT INTO TWO BYTES
26 B1=INT(Z/256)
27 B2=Z-(B1*256)
28 PRINT HEX$(B1)TAB(3)HEX$(B2)TAB(5)" = ";
30 GOSUB 500
35 REM /2 TO SHIFT RIGHT
40 Z=Z/2:NEXT
50 END
500 REM PRINT BITS
501 ZZ=INT(Z/256):GOSUB 510
502 ZZ=Z-ZZ*256:GOSUB 510
503 PRINT:RETURN
510 FOR ZB=7 TO 0 STEP -1
520 IF ZZ AND ZB(ZB) THEN PRINT"1"; ELSE PRINT "0";
530 NEXT
540 RETURN
1000 REM INIT BIT ARRAY
1010 FOR ZB=0 TO 7
1020 ZB(ZB)=2^ZB
1030 NEXT
1040 RETURNAnd it displays:

Success!
I could now incorporate that routine into my code, and take the data for one 8×8 character (like the solid circle I started this article with) and end up with 16 8×8 characters representing each position it could be within a 2×1 block of characters.
2010 DATA 60,126,255,255,255,255,126,60
In conclusion…
Wow. That was a really long way to go to show multiplying by 256 and dividing by 2, wasn’t it? But maybe there are some useful routines in these examples.
And now it’s my turn to ask you:
- Do you know a better/faster way to print 16-bit values in binary?
- Do you know a faster way to combine two 8-bit values into a 16-bit value, or split a 16-bit value into two 8-bit values?
- Is there a better/faster way to to bit shifting than multiplying or dividing by powers of 2?
Let me know in the comments, and maybe there will be a part 2 on this topic.
Until next time…


In case you haven’t looked it up yet, AND, OR, and NOT (yes, this does a bitwise complement) work on 16 bit signed values. So they’ll work from -32768 to 32767. That’s also why “true” is -1 and “false” is 0 – true is all bits set and false is no bits set. That allows bitwise AND, OR, and NOT to work in a boolean context.
Also, it should be faster to multiply by 0.5 than to divide by 2. Same goes for other powers of 2. This is especially true if you have the relevant value in one of the first variables you define in the program.
Also, you technically need the “INT()” after doing the divisions or you end up with fractions. Remember there is no integer division operation in Color Basic.
Awesome! Especially about the “why” of -1.
If someone just needs the low byte of a 16 bit value it might be not necessary to use INT(). This INT conversion is implicitly done by the interpreter if the value is given to some other commands (where expecting an integer), like POKE, or position parameters of string commands like MID$, LEFT$, RIGHT$, …
Great tip!
In case of on-bit-shift to left it could be faster to use
40 Z=Z+Z:NEXT
instead of
40 Z=Z2:NEXT
This operation (saves around 20 %).
I slightly better performance has Z=ZT if T is (an early) predefined variable with value 2 or for right shifts with 0.5. Especially for 0.5 this saves relatively much time, even in comparison to Z=Z*.5 (omitting digit 0). Converting constants is always expensive (because of parsing all the numberparts and the conversion to a float value).
Thanks! I’ll have to do a follow up.
Let’s pretend that C on the CoCo has stdint.h. Then
union {
uint16_t ui;
char byte[2];
} val;
is one way to get what you were doing with separate variables. To multiply by 256, just shove the least significant byte into the most significant byte and zero out the least significant byte; to divide by 256, go the other way around. Sadly, C doesn’t have a standard way of knowing whether the target is big or little endian, and it doesn’t carry over to Color BASIC.
Both Color BASIC and BASIC09 evaluate the STEP value just once, so “FOR N=1 TO 128 STEP N” won’t iterate over powers of two, but OTOH, you’re really using the values in another loop–use strength reduction and don’t bother to keep them in an array–OK, you’re going in descending order. Shucks; that turns it into a divide rather than just an add, and there’s no built-in function to reverse a string. Reversing it in BASIC might well be slower overall.
BASIC09 doesn’t have a binary format for PRINT USING, darn it. Seems like overkill to PRINT USING in hex to a pipe, read the pipe, and index an array of strings by the hex digit value to get the binary equivalent.
I tried the following for the “print a byte in binary” subroutine–no idea whether it sped or slowed the result. It assumes that up top you have
B$=”01″
then…
600 MASK=128
610 FOR BN=7 TO 0 STEP -1
620 PRINT MID$(B$,1-((BYTE AND MASK)<>0),1);
630 MASK=MASK/2
640 NEXT
650 RETURN