Updates:
- 2022-12-09 – Fixed program listing.
There is an interesting hidden message embedded in the Color BASIC ROM, and here is the code that reveals it:
0 REM COLOR BASIC EASTER EGG
10 A=26493:B=66:C=13:GOSUB40
20 A=291227:B=B+2:C=C+3:GOSUB40
30 END
40 I=RND(-A):FOR I=1 TO 4:PRINT CHR$(B+RND(C));:NEXT:RETURNIf you run this code, it will display this:
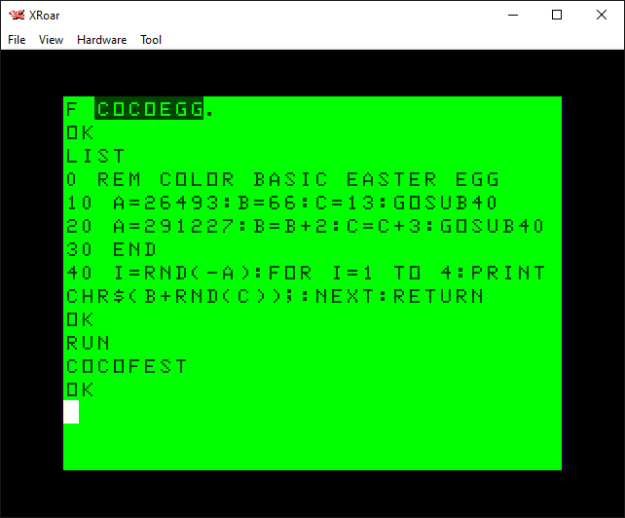
Amazing, eh? How did they possibly know back in 1980 that COCOFEST would become a thing?
But actually, it’s just a random message, and not a hidden message at all. I learned of this trick from this video by 8-Bit Show and Tell that claims to share a hidden anti-Microsoft Easter egg in Commodore 64 BASIC… and then reveals how the prank works.
If you tried to run that program on other flavors of BASIC, it probably would not work. It certainly does not produce the expected results on a CoCo.
10 A=125708:GOSUB 20:A=33435700:GOSUB 20:A=17059266:GOSUB 20 20 A=RND(-A) 30 A=INT(RND(A)*22):IF A THEN PRINT CHR$(A+64);:GOTO 30 40 PRINT:RETURN
This was the first video from 8-Bit Show and Tell I ever saw, and it’s lead me down quick a rabbit hole trying things he demonstrates on the Commodore computers on our beloved CoCo. And it all started with this random video that YouTube randomly showed me.
Monkeys and Shakespeare
The infinite monkey theerem states that…
“…a monkey hitting keys at random on a typewriter keyboard for an infinite amount of time will almost surely type any given text, such as the complete works of William Shakespeare.”
Wikipedia
We are just using BASIC’s RND() random number generator to simulate a monkey at a typewriter, and using short words instead of the complete works of Shakespeare.
It’s much quicker this way.
As previously discussed, the RND function generates a series of numbers that are not random. Each time you power up a CoCo, for instance, this code will produce the same “random” numbers the first time you run it:
FOR A=1 TO 8:PRINT RND(50);:NEXT
Try it for yourself using the web-based JS Mocha CoCo emulator.
In order to change the series of numbers, you pass a negative value into the RND() function, and that series will be used. If you do X=RND(-1), you will then get the same series of random values every time. If you do X=RND(-42), you get a different set of random numbers every time.
Magic!
Or math. But math is hard, and magic is just frustrating.
The monkey simulator
But how do you find which random seed value will give you the random numbers you want in the order you want them? The original prankster used brute-force trial and error.
A program can be designed that first seeds the RND function with -1, then generates a series of random numbers and tests to see if they are what it is looking for. In the case of the C64 version, it needed to see the numbers that represented the characters of the word followed by a ZERO to terminate the string.
If it did not work, it tries a seed of -2, and so on. This could take hours or days, and there is no guarantee the exact series of numbers will be found.
I decided to write a CoCo version of this monkey typewriter simulator, but I made some changes.
- First, I figured looking for “W”+”O”+”R”+”D” was more work than just looking for “W”+”O”+”R”+”D” without a 0 byte at the end. That should speed up the search, but require an extra bit of data in the display program since it now needs to know how many random values to use (the length of the word).
- The C64 version looked from A to the highest letter used (“BILL GATES SUCKS” scans A to U, though it doesn’t really need to try to find A since the earliest letter is B.) I figured that looking for A to Z (worst case, 26 choices) would be more work than just looking at the range of letters actually used in the word. For instance, finding “ABC” in a repeating random series of 26 numbers seems less likely than finding “ABC” if you were only using 3 random numbers. I made my generator look for a range covering only the letters being used. “CAT” would need numbers from “C” to “T”. “DOG” would need “D” to “O”. “ALACAZAM” would need “A” to “Z”. This meant my display program also needed to know the starting letter value and range value, in addition to the word length.
My version is not as clean and tidy as the C64 original
Here is the program I came up with. You can type in a word and it will present the range of letters it will look for, and then start searching until it finds it (or, weeks later, it has not and you give up):
10 REM rndwords.bas
20 POKE 65495,0
30 INPUT "TARGET STRING";T$
40 TL=LEN(T$)
50 IF TL=0 THEN 30
60 REM FIND LOWEST AND HIGHEST LETTER
70 LL=255:HL=0
80 FOR P=1 TO LEN(T$)
90 V=ASC(MID$(T$,P,1))
100 IF VHL THEN HL=V
120 ?V,LL;HL
130 NEXT
140 REM CALCULATE LETTER RANGE
150 R=HL-LL+1
160 PRINT "SEARCHING FOR: ";T$
170 PRINT "LETTER RANGE :";R;"(";CHR$(LL);" - ";CHR$(HL);")"
180 REM SEARCH...
190 FL=LL-1
200 FOR SD=1 TO 9999999
210 V=RND(-SD):A$=""
220 A$=A$+CHR$(FL+RND(R))
230 IF LEN(A$)<TL THEN 220
240 IF A$=T$ THEN PRINT -SD,T$
250 NEXT
1000 V=RND(-26493):FOR I=1 TO 4:PRINT CHR$(66+RND(13));:NEXT
Some words are found almost instantly. “HI” shows up immediately:

The output shows the random seed to start with (-5), the word it was looking for (“HI”), the ASCII character to add to the random numbers it finds, and the range to use in the RND functions.
To display the string back, you would modify my original COCOFEST program with the proper values, or do it manually:
V=RND(-5):FOR I=1 TO 2:PRINT CHR$(71+RND(2));:NEXT:PRINT
Here are some words I have found:
REM "COCO"
V=RND(-26493):FOR I=1 TO 4:PRINT CHR$(66+RND(13));:NEXT
REM "FEST"
1001 V=RND(-291227):FOR I=1 TO 4:PRINT CHR$(68+RND(16));:NEXT
REM "SUB"
1002 V=RND(-56403):FOR I=1 TO 3:PRINT CHR$(65+RND(20));:NEXT
REM "ETHA"
1003 V=RND(-1049135):FOR I=1 TO 4:PRINT CHR$(64+RND(20));:NEXT
I tried to find “COCOFEST” together, but after days and days of running, it still hadn’t. Perhaps it would have found it if I was searching the entire A-Z range versus just C-T. It’s random-ish, after all.
Perhaps one of you will take this concept and recreate the C64 version, looking for A-Z and a zero. Maybe that works better. I did not try.
Perhaps one of you will start compiling a dictionary of random words and we can use this as a secret decoder ring for passing cryptic messages to each other on Facebook.
Perhaps this will just be a passing random thought and we will never speak of it again.
But knowing me and this site, I expect we will speak of it again. Especially if I get any good comments to this post.
Until next time…

